Le développement des récepteurs de lumière a amené à reconsidérer la notion de magnitude. Des méthodes précises de mesure de la luminosité absolue ont établi que l'ancienne classification correspondait approximativement à une échelle logarithmique. Ceci est typique de la façon dont nos sens perçoivent les sensations tels l'intensité des sons la hauteur d'une note de musique, etc. En d'autres mots, c'est ainsi que chaque fois que nous avons l'impression qu'une étoile parait 2 fois plus brillante qu'une autre, le rapport des intensités lumineuses de ces étoiles est en réalité d'environ 2,5 à 1.

Afin que la nouvelle échelle de magnitude soit le plus près possible de l'ancienne, il fut convenu qu'une différence de cinq magnitudes correspondrait à un rapport d'intensité lumineuse de 100 et que les paliers entiers ainsi définis sont dans des rapports égaux.

Mathématiquement, nous aurons alors:

Si on considère deux étoiles de luminosité La et Lb , la différence de magnitude entre elles s'établit comme suit:

NOTE: Cette dernière relation s'appelle loi de Pogson.

L'exposant est mb ma et non l'inverse, parce que la convention veut que plus une magnitude est élevé, plus la source lumineuse est faible. Aussi, dans le dernier terme de droite [2,5 log(La/Lb)] se rappeler que le chiffre 2,5 est exact. Il ne s'agit pas du 2,512 que l'on aurait tronqué en biffant les deux dernières décimales. Selon mon expérience, cette coïncidence est souvent la source de confusion.

Par ailleurs, on sait que l'oeil nu moyen, par une nuit sans lune et loin de la pollution lumineuse, voit jusqu'à la sixième magnitude. Un télescope verra donc jusqu'à:

Comme autre relation utile, mentionnons que le rapport des diamètres D2/D1 entre deux télescopes qui auraient une différence de magnitude limite égale à un, serait égale à la racine carrée du rapport de leur surface, soit:

L'expression générale est:

VITESSE OPTIQUE OU OUVERTURE

Ce chiffre est simplement le rapport F/D où F est la longueur focale de l'objectif et D son diamètre. Cette notion est généralement bien comprise par ceux qui font de la photographie, mais j'ai l'impression qu'elle n'est pas claire chez tous les astronomes.

Soit deux lentilles L₁ et L₂ dont le diamètre et la longueur focale sont le double l'une de l'autre.

Nous aurons alors:

Ces deux lentilles ont la même vitesse optique. Elles formeront donc des images de même luminosité. Est ce possible me direz vous? Votre intuition vous suggère que la lentille de plus grand diamètre doit être plus lumineuse!!

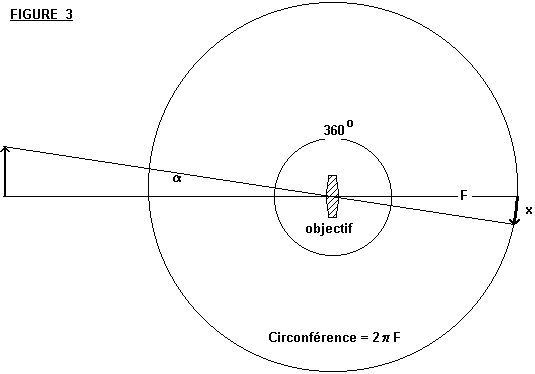
Soit une lentille de focale F. Imaginons qu'il s'agit d'une lentille super grand angle capable de cerner tout l'horizon, soit 360 degrés. L'image obtenue serait alors un cercle de circonférence égale à 2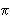F.

A partir de la figure 3, nous pouvons établir l'équation suivante:

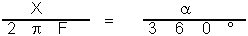
où

F = focale du télescope
X = dimension linéaire de l'image de l'objet observé
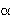= angle en degrés sous tendu par l'objet observé

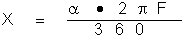
Dans le cas de la lune et du soleil, leur diamètre angulaire est approximativement de 0,5 degré. Nous obtenons alors:

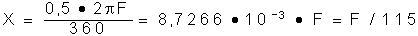
Pour les planètes ou les étoiles doubles, nous utilisons plûtot la seconde d'arc comme unité. La formule devient alors:

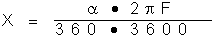où 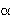est en seconde d’arc.

Soit Jupiter dont le diamètre à l'opposition est d'environ 40 secondes d'arc. Au foyer d'un télescope de 152mm (6 po.) ayant une focale de 1200mm (48 po.), nous aurons:

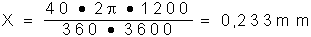
Je suppose que vous vous êtes remis de la surprise que vous avez eue lorsque, après avoir photographié une planète pour la première fois, vous n'avez trouvé qu'un point sur votre négatif. Vous voyez pourquoi il en était ainsi. Heureusement, on peut améliorer la situation en projetant l'image formée au foyer primaire au moyen d'un oculaire qui en donne une image agrandie par un facteur d'environ 4 à 10, en pratique. Pour plus de détails sur cette technique de projection, consultez un ouvrage sur la photographie astronomique ou un amateur expérimenté.

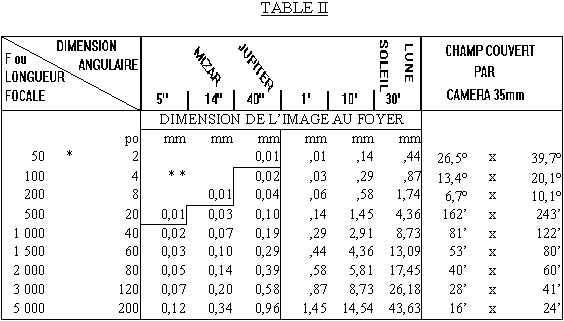
La table II donne la dimension linéaire X d'une image formée au foyer primaire d'un télescope en fonction de la dimension angulaire de l'objet. La dernière colonne, donne le champ angulaire total que peut couvrir une pellicule de format 35 mm. Pour le calcul, on reprend l'équation de base précédente que l'on transforme pour obtenir:

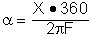où X est une des deux dimensions de la pellicule, soit 24 mm C 36 mm pour une caméra dite de format 35 mm.

* Correspond à la lentille normale d'une caméra 35mm.

* * A toute fin pratique, la limite minimum de 0,01 mm est basée sur le fait qu'après agrandissement jusqu'à 20 x 25cm (8 x 10 po.), la dimension de l'image est d'environ 0,1 mm, ce qui correspond approximativement aux plus petits détails visibles sur une telle photographie.

D'après les données de la table II, on constate que plusieurs étoiles doubles devraient être résolues sur des photographies prises avec nos télescopes d'amateurs. Je crois qu'il y aurait matière pour des travaux intéressants. J'espère éventuellement lire vos résultats dans des revues adressées aux astronomes amateurs.

POUVOIR SÉPARATEUR

Dans les traités d'optique, nous lisons qu'une source ponctuelle située à l'infini forme, au foyer d'un objectif circulaire, une tache de diffraction de rayon:

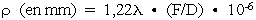Équation ...a)

où

F/D = vitesse optique du système. F et D ont les mêmes unités. Mais comme on veut exprimer 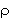en mm, on exprime également F et D en mm.

N.B.: Il est hors du cadre de cet article de démontrer la relation précédente.

Considérons deux étoiles dont l'image au foyer consiste en fait à deux cercles de diffraction de rayon 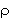En supposant que la distance angulaire entre ces deux étoiles devient de plus en plus petite, il arrive un moment où les deux cercles vont se confondre et nous ne pourrons plus séparer les deux composantes. L'étoile double nous apparaîtra alors comme une étoile simple.

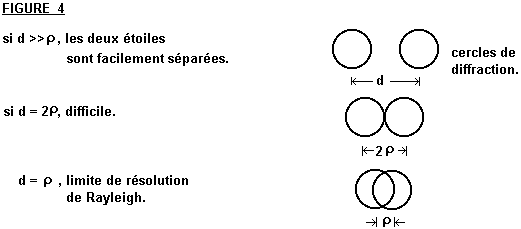
Lorsque la distance centre à centre est égale à 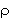, l'image ressemblera à un huit ou tout au moins à une étoile allongée. Lorsque d est plus petit que 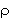, il n'est plus possible de décider de la dualité de l'étoile. Le pouvoir séparateur correspond donc à d = .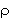

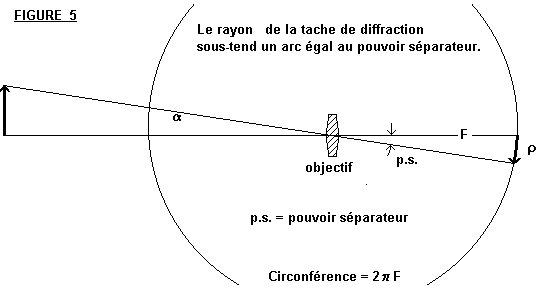
Imaginons que notre objectif (lentille) est au centre d'un cercle de rayon F. Le rayon 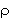de la tache de diffraction divisé par la circonférence 2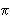F sera égale à l'angle p.s. divisé par 360 degrés. En fait, le raisonnement suivi ici est à l'inverse de ce que nous avons fait à la partie 4.

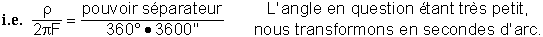
Pouvoir séparateur = 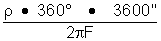Équation ...b)

En substituant l’équation a) dans b), nous obtenons:

Pouvoir séparateur =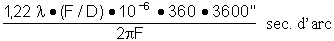

Pouvoir séparateur =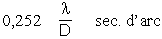

Appliquons la relation précédente au cas de la lumière jaune (milieu de la bande visible) où 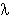= 560nm.

Pouvoir séparateur = 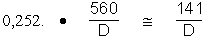sec. d'arc

On se rappellera que le diamètre D est en mm. Pour les vieux d'entre nous, nous aurons en pouces: Pouvoir séparateur = 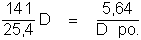sec. d'arc

Note: Pour un excellent article sur le pouvoir séparateur des télescopes, voir SKY & TELESCOPE du mois de février 1983, page 176.

Comme nous l'avons vu dans le chapitre 1, le grossissement d'un télescope consiste en fait à agrandir le diamètre angulaire des objets observés. Notre oeil pourra donc résoudre un objet si le diamètre angulaire d'un objet multiplié par le grossissement G est au moins égal à 6 min. d'arc.

D'autre part, nous avons déjà établi que le pouvoir séparateur d'un télescope était limité par la relation:

Pouvoir séparateur = (141/D) sec. d'arc; où D est le diamètre de l'objectif en mm.

En divisant le pouvoir séparateur de l'oeil par celui de notre télescope, nous obtenons le grossissement qui nous permettra d'utiliser pleinement la performance de notre instrument. C'est le grossissement maximum utile parce qu'au-delà nous obtenons seulement des taches de diffraction plus grosses, mais non mieux séparées entre elles. On dit alors que c'est un grossissement sans valeur parce qu'il ne permet pas de voir mieux.

G max = 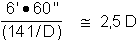où D est le diamètre de l'objectif en mm.

Si D est en po., on obtient : G max 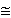60D.